Математика футбольного м'яча

Про те, чому офіційний м'яч останніх чемпіонатів світу насправді куб.

Здавалося б, м'яч - предмет круглий, що ще про нього сказати? Але реальність не така проста, як здається, і на те, щоб підвищити «сфероподібність» футбольного м'яча, виробникам довелося чимало потрудитися. І ось уже шостий рік м'яч офіційних турнірів ФІФА - куб. Чому це так?




Поверхня класичного футбольного м'яча складається зі злегка викривлених 12 правильних п'ятикутників чорного кольору і 20 правильних білих шестикутників.

«Класичним» такий м'яч був не завжди: вперше такі крій і розфарбування були використані для офіційного м'яча на чемпіонаті світу в 1970 році в Мексиці. Чорно-біла гама тоді була обрана з міркувань контрастності, щоб м'яч було краще видно на екранах чорно-білих телевізорів, що переважали в той час. Та й саму свою назву - Telstar - він отримав на честь телевізійного супутника. У наступні роки розфарбування офіційних м'ячів змінювалося, але крій залишався незмінним аж до чемпіонату 2002 року.

З точки зору математики класичний футбольний м'яч є усіченим ікосаедром.

Ікосаедр - один з п'яти правильних багатогранників. Його назва походить від давньогрецьких слів «двадцять» і «основа». У ікосаедра 12 вершин, 20 граней - правильних трикутників, 30 ребер.


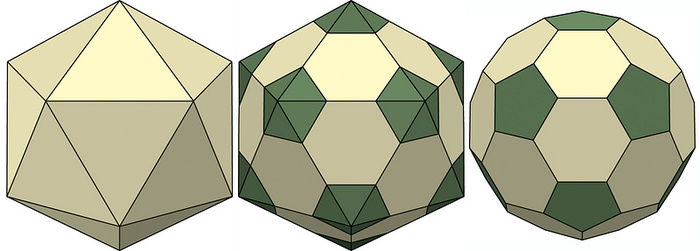
Якщо зрізати верхівки ікосаедра, відступивши від вершин так, щоб частини граней, що залишилися, були правильними шестикутниками, то зрізи будуть правильними п'ятикутниками. Це усічений ікосаедр - один з напівправильних багатогранників: всі грані - правильні багатокутники декількох різних типів, всі вершини влаштовані «однаково», тобто багатогранні кути при вершинах рівні.

Отже, класичний футбольний м'яч - усічений ікосаедр.




Як відомо, сферу не можна зігнути з плоскої розгортки. Це забороняє зробити математика - теорема про те, що важлива характеристика поверхні, звана гауссовою кривизною, не змінюється при згинанні без розтягнень.

Гауссова кривизна відображає внутрішню геометрію поверхні і не змінюється при її згинанні. Наприклад, у площини гауссова кривизна дорівнює нулю. У циліндра і конуса, які можна згорнути з плоского аркуша паперу, - теж нуль.

А ось у сфери гауссова кривизна позитивна. Значить, зробити сферу з плоских панелей (розгортки) - неможливо. І навпаки, розгорнути сферу на площину без спотворень теж не можна, і всі плоскі карти Землі - неточні.

Тому яку модель м'яча не взяти, її необхідно «роздувати». А чи можна придумати модель м'яча, що складається з плоских панелей, але вже від початку ближчу до сфери, ніж класична? (Зрозуміло, що можна взяти багатогранник з великим числом граней і вершин, але тоді ускладниться процес виготовлення.)

Після 2002 року почалися експерименти, і в 2014 році на чемпіонаті світу в Бразилії відбулася прем'єра нового офіційного м'яча, що отримав назву Brazuca.

Модель цього м'яча дійсно більш «сфероподобна», ніж класична. Але при цьому Brazuca - це куб!

Як і куб, вона збирається з шести однакових плоских панелей, що мають по чотири кути. У неї вісім вершин, в кожній з яких сходиться по три панелі.



Придумані фірмою Adidas панелі дійсно можна склеїти в опуклу поверхню. Успіх гарантує виконання умов теореми: сума кутів панелей в вершинах не перевищує 360 градусів, довжини «сторін» панелей між кутами збігаються, а сума кривизн кордонів в точках склейки невід'ємна.

У моделі класичного м'яча вся кривизна зосереджена в кінцевому числі «виступаючих» вершин. Всі чотири кути панелі Brazuca рівні 120 градусам. Відповідно, коли в вершинах моделі зустрічаються три кути, сума кутів навколо вершини дорівнює 360 градусам: поверхня м'яча навколо вершини буде «плоскою».



Але куди ж поділася кривизна? Адже сфера є поверхнею постійно позитивної кривизни і кривизна повинна бути! У моделі бразукі кривизна «розмазана» по довгих ребрах - через це модель стає істотно ближчою до сфери, ніж модель класичного м'яча.

---

© знайдено в мережі