Сучасні математики розв'язали задачу, якій близько 2500 років

Її вигадав ще грецький математик Анаксагор близько 450 року до н. е., а розв'язали її троє математиків з Канади та Великої Британії за допомогою новітніх методів геометрії. Троє математиків вперше показали, як сформувати квадрат такої ж площі, як і коло, розрізавши їх на взаємозамінні частини, які можна візуалізувати.

Вчені Андраш Мате та Олег Піхурко з Ворицького університету (University of Warwick) та Джонатан Ноель з Університету Вікторії (University of Victoria) вирішили давнє завдання «квадратури кола», яке вигадав грецький математик Анаксагор близько 450 року до н. е.

Близько 2,5 тисяч років тому Анаксагор із Клазомен мав час подумати. Грецький математик сидів у в’язниці за те, що стверджував, що Сонце не бог, а розжарена скеля розміром із півострів Пелопоннес. Філософ, який вважав, що «розум править світом», використав своє ув’язнення, щоб впоратися з відомою нині математичною проблемою, відомою як квадратура кола: чи можна за допомогою циркуля та лінійки створити квадрат, площа якого дорівнює заданому колу?

Дивно, але математики досі працюють над цим питанням. І вони просуваються вперед. Стаття, опублікована минулого тижня в Інтернеті Андрашем Мате, Олегом Піхурком та Джонатаном Ноелем є останньою, яка приєдналася до цієї давньої традиції. Автори показують, як коло можна звести в квадрат, розрізавши його на частини, які можна візуалізувати та, можливо, намалювати. Це результат, який базується на багатій історії.


Ілюстрація Анаксагора в червоному капелюсі та жовтому сюртуку з Нюрнберзької хроніки. Грецький математик Анаксагор із Клазомен, зображений тут як середньовічний вчений у Нюрнберзькій хроніці, був першим, хто написав про «зведення кола в квадрат» — оманливо складну проблему.

Точну відповідь на запитання, поставлене Анаксагором, було дано в 1882 році, коли німецький математик Фердинанд фон Ліндеманн довів, що квадратура кола неможлива за допомогою класичних інструментів. Він показав, що пі — площа кола з радіусом 1 — є особливим видом числа, яке класифікується як трансцендентне (категорія, яка також включає число Ейлера, e). Оскільки попередній результат продемонстрував, що неможливо використовувати циркуль і лінійку, щоб побудувати довжину, що дорівнює трансцендентному числу, також неможливо звести коло таким чином у квадрат.

На цьому історія могла б закінчитися, але в 1925 році Альфред Тарскі відновив проблему, змінивши правила. Він запитав, чи можна виконати завдання, розрізавши коло на кінцеву кількість частин, які можна було б переміщати в межах площини та знову зібрати в квадрат однакової площі — підхід, відомий як еквідекомпозиція.

Іншими словами, два об’єкти є рівноскладними, якщо їх можна розбити на шматки однакового розміру та форми, або, точніше, «якщо ви можете розбити їх на скінченну кількість частин так, щоб відповідні частини були конгруентні одна одній».

Стаття 1964 року була першою, яка суттєво просунулася у версії проблеми Тарскі. Автори показали, що композицію неможливо зробити за допомогою ножиць. Завдання, якби це було можливо, вимагало б більш складних фрактальних фрагментів, пронизаних дірками та хитромудро зазубреними краями.

Так було до 1990 року, коли Міклош Лачковіч відповів на запитання Тарського однозначним «так»: коло можна перетворити на квадрат.

Щоб візуалізувати досягнення Лачковича, уявіть коло та квадрат поруч на сторінці. Він продемонстрував, що якщо коло розділити щонайбільше на 1050 частин, усі вони складні та незвичайної форми, ці частини можна переміщати — навіть не обертаючи — доки вони повністю не заповнять квадрат.



Але щоб досягти цього результату, Лачковіч не працював з формами. Замість цього він перетворив проблему геометрії в задачу теорії графів. Він взяв великий граф із двома окремими наборами вершин — один відповідає колу, інший — квадрату, а потім встановив взаємно-однозначну відповідність між вершинами в одному наборі та вершинами в іншому.

Стен Вагон, математик з коледжу Макалестер, описав результати як «приголомшливі». Лачкович показав, як «взяти круглий простір і зробити його прямим».

Однак була заковика. Доказ Лачковича є доказом існування, який математики називають «неконструктивним». Він довів, що це можливо, але він не міг сказати, як побудувати частини, і не міг їх описати. Гірше того, шматки «невимірні», що означає, що неможливо визначити їхню площу.


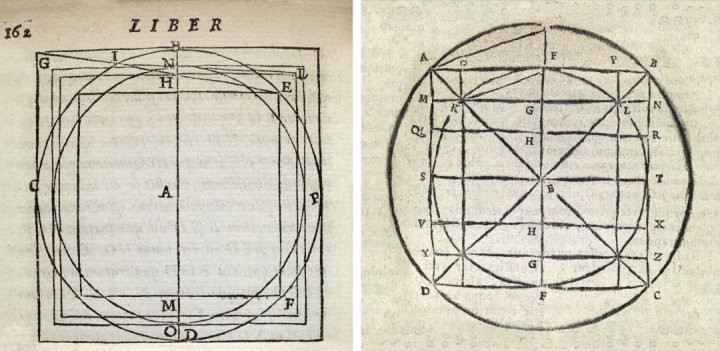
Дві діаграми, що показують кола та квадрати, накладені один на одного, з літерами, що позначають перетини та сегменти
Після століть зусиль — ці діаграми датуються 16-м і 17-м століттями — Фердинанд фон Ліндеманн довів, що неможливо накреслити квадрат рівної площі заданому колу, використовуючи лише циркуль і лінійку. Але якщо нам не потрібні ці інструменти, проблема набуває нового життя.

Наступний великий крок був зроблений десятиліттями пізніше в статті, опублікованій у січні 2016 року Лукашем Грабовським, Мате та Піхурко. Їхні докази, на відміну від Лачковича, є майже повністю конструктивними, що означає, що фрагменти здебільшого чітко визначені. Але знову була заковика: ті чітко окреслені фігури з кола не заповнюють весь квадрат. Додаткові частини все ще необхідні, щоб покрити крихітну частину квадрата. Ця частина настільки крихітна, що не має площі, і математики називають її «набором міри нуль».

«Майже про весь простір подбали», — сказав Ендрю Маркс, математик з Каліфорнійського університету в Лос-Анджелесі. Ви не можете навіть намалювати відсутні частини, сказав він, оскільки набір виглядатиме невидимим.

Незважаючи на ці необхідні додаткові деталі, результат був драматичним кроком вперед, сказав Маркс. «Вони знайшли спосіб звести коло в квадрат, який спрацював майже скрізь — скрізь, крім набору нульової міри».

Рік потому Маркс разом зі Спенсером Унгером, який зараз працює в Університеті Торонто, зробили значне вдосконалення, надавши перший повністю конструктивний доказ квадратури кола — той, який працює всюди без винятку. Їх стаття містить повний опис усіх частин, необхідних для квадратури кола. «Їхні твори кращі», — сказав Мате. «У них немає цього потворного набору нульової області».

Тим не менш, їхні докази включають навіть більше частин — близько 10200 — і ці частини все ще досить складні. «Недоліком нашої роботи є те, що, незважаючи на те, що частини чітко визначені з математичної точки зору, їх дуже важко уявити», — сказав Маркс.

Це залишило певний простір для вдосконалення, чого й досягли Мате, Ноель і Піхурко. Їхні деталі, знову ж таки налічуючи близько 10200, мають простішу форму, і їх набагато легше сприймати для візуалізації математикам.

Але це ще не кінець історії. «З цією проблемою ще потрібно зробити багато математики», — сказав Олександр Кекріс, математик із Каліфорнійського технологічного інституту. «Це процес».

У Піхурка вже є ідеї щодо подальшого спрощення частин, зменшення їх загальної кількості та зменшення нерівностей. І Маркс провів комп’ютерні експерименти, які припускають — але не доводять — що еквідекомпозицію можна здійснити з 22 частин. Він вважає, що мінімальна кількість, швидше за все, ще нижча.

«Я б побився об заклад на пиво, що ви можете скласти коло, маючи менше ніж 20 елементів», — сказав він. «Але я б не поставив на це 1000 доларів».

---

© за матеріалами