Що таке кінетичне мистецтво і як воно працює (відео)

Архітектура - застигла музика. Цей відомий вираз, який приписують німецькому філософу і теоретику мистецтва Фрідріху Шеллінгу, стосується «великої» архітектури. Однак з середини XX століття художники все більше тяжіють до особливих «малих» архітектурних форм - кінетичних скульптур, які застиглими назвати вже не можна. Навпаки, ці скульптури, окремі елементи яких, взаємодіючи, переміщаються химерними траєкторіями, заворожують глядача постійним рухом. Про кінетичні скульптури пишуть книжки мистецтвознавці, сперечаються відвідувачі виставок. Спробуйте поглянути на кінетичні скульптури під іншим кутом - очима математика.



Нідерландський художник (народився в 1948 році), відомий своїми «штучними формами життя» - скелетоподібними фігурами, здатними пересуватися піщаними пляжами під дією сили вітру. Генетичні алгоритми Янсена здатні симулювати біологічну еволюцію видів.



У роботах Тео Янсена знаходять застосування ідеї стопоходячих машин, основний вузол яких переводить обертальний рух в поступальний. Скульптури Янсена нагадують химерні істоти, які спритно перебирають десятками ніг і з легкістю рухаються під дією вітру. Сам художник називає їх «пляжними звірами», Strandbeest. Однак насправді навчити «звірів» ходити не спотикаючись не так і просто - необхідно не тільки коректно спроектувати кожну ногу, але і організувати їхню спільну роботу. Для цього скульптору потрібно вирішити систему нелінійних алгебраїчних рівнянь, що випливають з теореми Піфагора.



Ось конкретний приклад. Розглянемо два важелі 1 і 2, з'єднаних шарніром в точці 5. Припустимо, нам відомі координати кінців 3 і 4 і ми хочемо визначити місце розташування шарніра. Для вирішення цього завдання необхідно аналітично або чисельно вирішити систему двох нелінійних алгебраїчних рівнянь, де L1 і L2 - це гіпотенузи двох прямокутних трикутників (довжини важелів), а x4 - x5, y4 - y5, x3 - y5 і y3 - y5 - це довжини катетів . Як відомо, ці величини пов'язує між собою теорема Піфагора: квадрат гіпотенузи дорівнює сумі квадратів катетів.



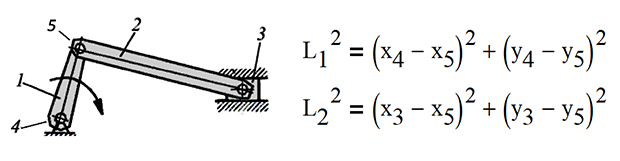
Зрозуміло, кожна «нога» містить більше двох шарнірів, а тому завдання, яке належить вирішити художнику перед проектуванням скульптури, набагато складніше. Так чи інакше, воно зводиться до оптимізації вузлів - тобто підбору таких довжин важелів, при яких конструкція буде рухатися плавно, без поштовхів. Нарешті, після того як скульптура буде спроектована, необхідно зробити оптимізаційні розрахунки на міцність і переконатися в тому, що вона не зламається. Тут стануть в нагоді знання, які акумулює легендарна наука за назвою опір матеріалів (або, як її скорочено називають студенти, «сопромат). І тільки після проведення всіх розрахунків скульптор може братися за інструменти, щоб зібрати конструкцію з пластикових трубочок, дерев'яних брусків, скотча і поліетилену.

Механічні «звірі» Тео Янсена - це не просто ходячі машини, - вони запасають енергію вітру, надуваючи пружний «шлунок», що складається з пластикових пляшок, вміють визначати тип ґрунту, по якому ходять, і викидають якір, якщо вітер дме надто сильно. Все це вдається їм без залучення складної електроніки.




Американський художник, чия творча біографія налічує вже понад п'ятдесят років. Останні тридцять років він присвячує свої зусилля «вітряним скульптурам» (Wind Sculptures).



Роботи Лімена Уїтакера вимагають подуву вітру, від якого вони починають обертатися і створювати потрібний «естетичний» ефект. У його роботах використовуються закони аеродинаміки, а самі скульптури представляють собою своєрідні прилади для виміру швидкості вітру (анемометри, вітроміри).

Швидше за все, на створення мобілів Уітакера наштовхнуло обертання традиційного флюгера з анемометром у вигляді чотирьох півсфер, які використовують метеорологи. Втім, сам автор стверджує, що черпає натхнення в природі - в розгойдуванні трави і дерев під дією вітру. Сучасні комп'ютерні програми дозволяють моделювати геометрію обтікання газом або рідиною складних статичних або рухомих конструкцій, проте Уїтакер працює «з натхнення», визначаючи профілі кожного з «млинових крил» дослідним шляхом.



Обтікання тіла повітрям описується законом збереження енергії - потенційна енергія переходить в кінетичну і назад, але сума енергій залишається постійною. У газодинаміці потенційна енергія визначається тиском потоку, а кінетична - швидкістю потоку. Разом їх пов'язує формула, відкрита Даниїлом Бернуллі на початку XVIII століття. На малюнку видно, що швидкість потоку повітря над крилом вища швидкості потоку під крилом.


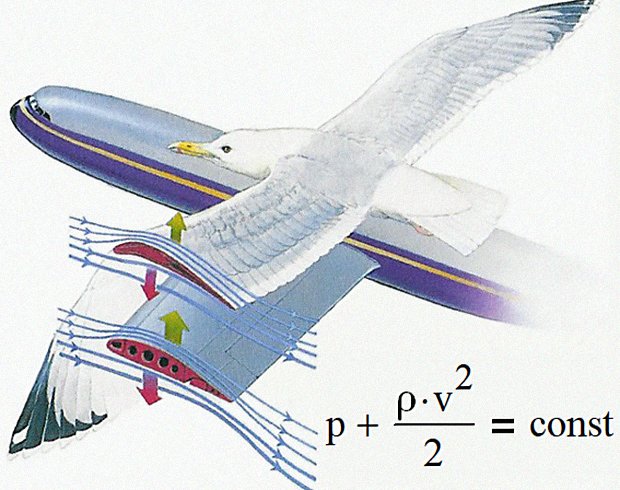
Перепад тисків під крилом і рівняння Бернуллі

Отже, через ефект Бернуллі тиск повітря над крилом буде нижчим. Це і є причина підйомної сили, яка змушує літак і птаха триматися на повітрі, а кінетичні скульптури Лімена Уїтакера - обертатися навколо своєї осі.




Американський художник, який народився в 1970 році в Каліфорнії, вивчав монументальний живопис у Флоренції, але згодом почав розробляти і збирати кінетичні фігури - головним чином з дерева.



Рубен Марголін доповнив механізми Тео Янсена, що базуються на класичній кінематики шарнірів і важелів, додавши до них нові зв'язки у вигляді... мотузочок. За допомогою таких механізмів також можна перетворити обертальний рух в прямолінійний, проте з точки зору математики їхнє моделювання набагато складніше.

Так само, як і в «класичних» стопоходячих машинах, тут необхідно вирішувати систему нелінійних алгебраїчних рівнянь. Нелінійність виникає тут внаслідок застосування теореми Піфагора (або теореми косинусів) до двох шарнірно зв'язаних важелів, які, як правило, і є «елементарним атомом» багатьох кінетичних скульптур. Якщо додатково використовуються і мотузки, то до важелів і шарнірів додаються блоки у вигляді коліщаток з жолобками на ободі.

Якщо ж потрібно враховувати не тільки кінематику, але і динаміку стопоходячих машин, то доводиться вирішувати і алгебраїчні, і диференціальні рівняння, що зв'язують силу F з масою m і прискоренням (другий закон Ньютона). А прискорення - це, як відомо, друга похідна шляху S від часу t: a = d2S / dt2.

Диференціальні рівняння вирішувати набагато складніше, ніж алгебраїчні, складніше і їхнє чисельне моделювання. Наприклад, в деяких випадках невелика помилка в початкових даних веде до істотної зміни траєкторій системи - цей ефект відомий як динамічний хаос. Втім, для класичних механічних систем така поведінка була б досить несподіваною.

Про художників, які працюють в області кінетичного мистецтва, а також про їхні роботи можна розповідати безконечно, але на цьому ми зупинимось. У світі є ще багато інших цікавих речей.

---

© за матеріалами