Скатертина Улама: найгарніша фундаментальна математична картина

1963 рік. На черговому семінарі польський математик Станіслав Улам відверто нудьгує. Замість того, щоб слухати доповідача, він креслить на папері сітку для шахового етюду, але замість цього починає нумерувати клітинки своєму зошиті по спіралі:

Чисто інтуїтивно Станіслав починає відзначати прості числа, тобто ті, які без остачі не діляться ні на які числа, крім себе і одиниці:



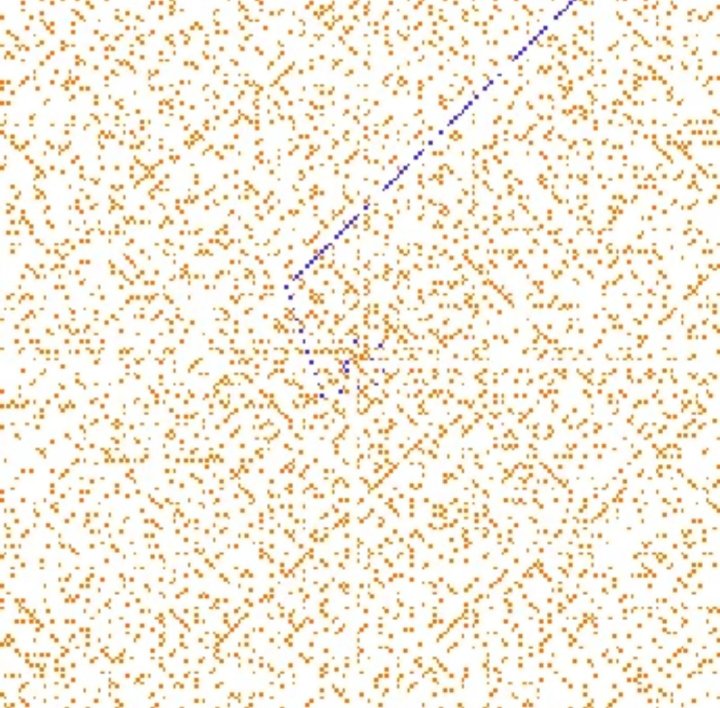
Вже навіть на такому невеликому малюнку йому стає ясно, що прості числа дивним чином вибудовуються по діагоналях або, як сказав Улам, "проявляли сильно невипадкову поведінку". Добравшись до інститутської ЕОМ, математик разом з колегами побудував цей патерн для 90 мільйонів чисел і отримав так звану скатертину Улама або спіраль простих чисел:



У чому математичне значення скатертини Улама?

Діагоналі, на яких лежать прості числа описуються квадратним тричленом виду: ax^2+bx+c, що дозволяє швидко виділяти такі многочлени, які породжують прості числа, що є важливим криптографічним завданням. Наприклад, ось відомий тричлен Ейлера: x^2+x+41, значення якого для будь-якого числа менше 40 є простим числом:



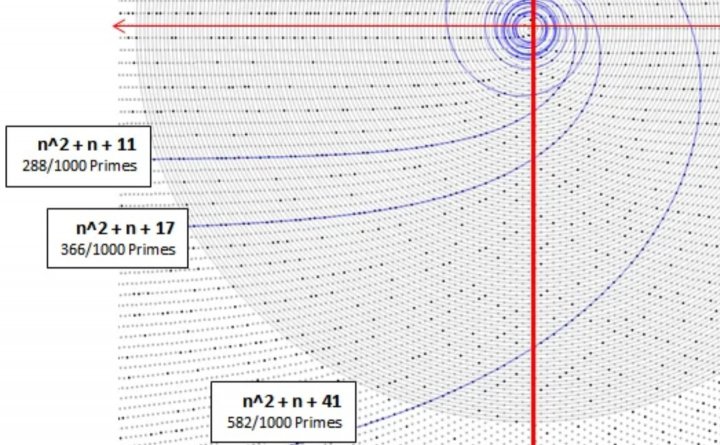
Пройшовши по шляху Улама, математики почали пропонувати інші, іноді навіть більш зручні, візуалізації. Наприклад, спіраль Сакса, побудована за наступним принципом в полярній системі координат. Для кожного числа його розташування на спіралі Сакса визначається відстанню r і кутом θ. Наприклад, для числа 16, радіус - це √16=4, а кут θ=2π*4=8π, тобто це число розташоване строго на схід. Якщо взяти більше чисел, вийде цікава картина:



У спіралі Сакса прості числа розташовуються на кривих лініях, які називаються "кривими добутків". Так як вони закручуються у нескінченність, з їх допомогою можна передбачати появу гігантських простих чисел, що дуже подобається криптографії, тому що чим більшим є просте число, тим важче "зламати" шифр, на основі якого він створений (дуже грубий опис).

---

© знайдено в мережі